VI. Mathematical Reasoning & Logic
It is important for students to be explicitly taught how to use reasoning and logical justification to communicate their ideas effectively.
Developmental Stages of Mathematical Proficiency
Numeracy is more than number sense and procedural fluency. It is the foundation upon which we see and represent the world. Numeracy opens doors to creativity, connection, critical thinking, and lifelong learning. Viewing the stages of development as nested and inclusive of each other helps reinforce the idea that working on productive challenges at any stage of the continuum supports further growth and understanding in other areas. Learners typically approach new ideas by recognizing that they are grappling with something new and then making comparisons to the knowledge they already have about a topic. This act of grounding oneself is integral to the process of acquiring new skills and knowledge. Scaffolding instruction to effectively build from one stage to the next is a key part of developing a structured, cohesive, and robust numeracy program.
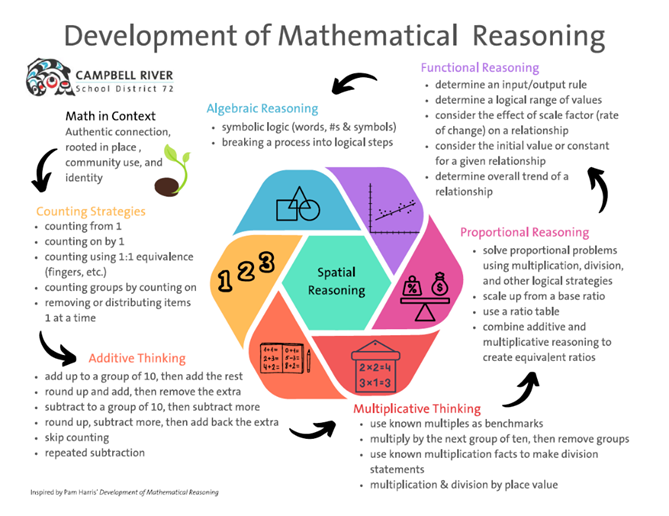
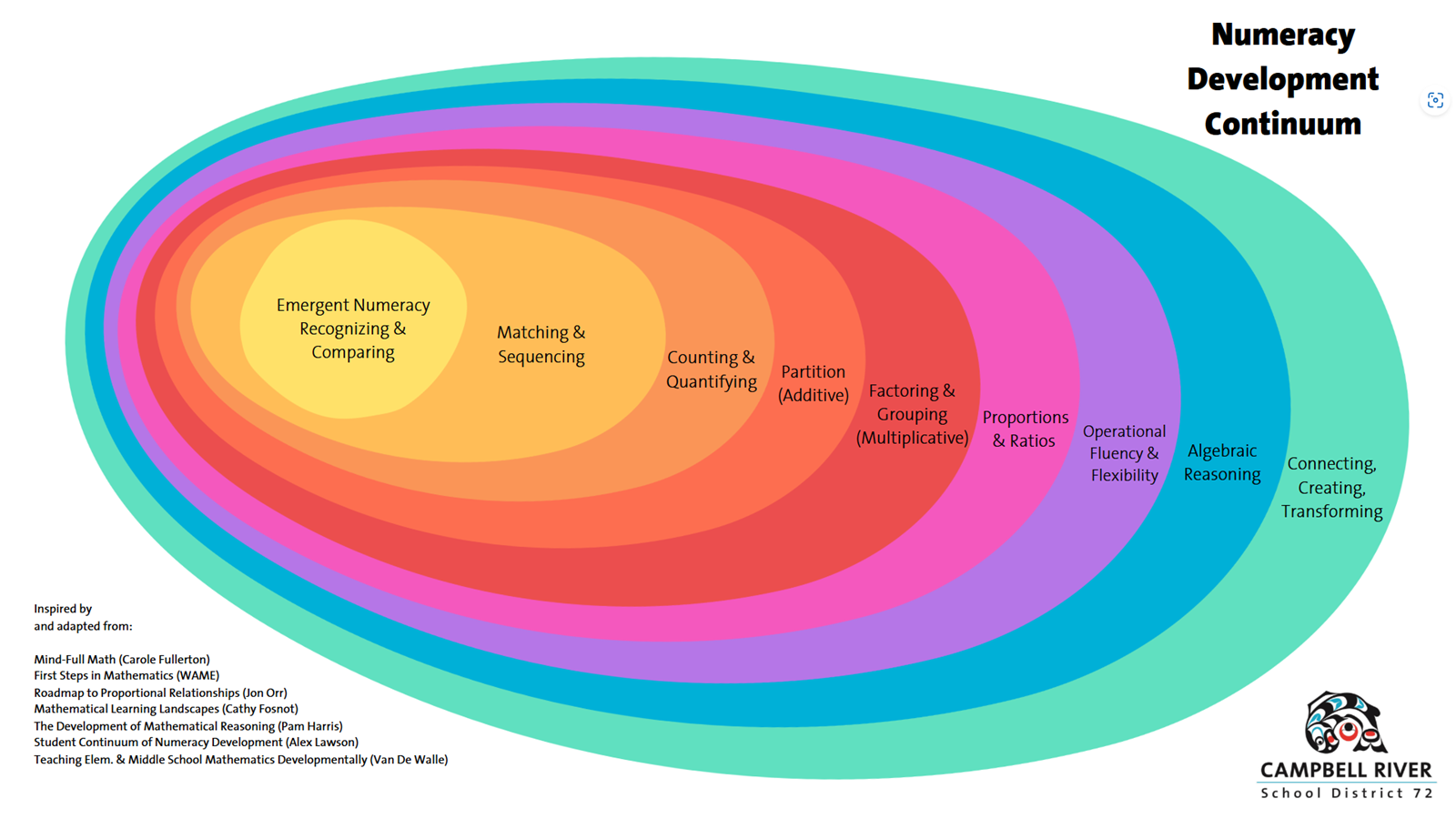 Numerate citizens have opportunities/solve problems/ find solutions using logic and reasoning. One way to visualize the development of numeracy is as a multi-step process with spatial reasoning and modelling as a central hub. Anchoring students’ learning to hands-on, real-world, and observable phenomena helps students to develop increasingly complex ways of thinking about mathematical ideas.
Numerate citizens have opportunities/solve problems/ find solutions using logic and reasoning. One way to visualize the development of numeracy is as a multi-step process with spatial reasoning and modelling as a central hub. Anchoring students’ learning to hands-on, real-world, and observable phenomena helps students to develop increasingly complex ways of thinking about mathematical ideas.
Concreteness Fading
Concreteness fading is an instructional method where learners are introduced to a concept through increasingly abstract representations, moving from concrete, tangible examples to more symbolic or generalized forms. This approach aims to enhance understanding and promote transfer of knowledge by first grounding the concept in familiar, concrete experiences and then gradually shifting to more abstract, symbolic representations.
Key Vocabulary and Notation for Math K-9
Reinforcement of key vocabulary can support student success in mathematics. In addition to traditional print glossaries (English and French), teachers have access to interactive, illustrated glossaries as well as locally developed logic games and puzzles.
| Resource Description | Resource Links | |
| 1 | Math glossary for teachers and students (K-8) | Math Glossary K-8 |
| 2 | Includes French to English and English to French Math Terms (PDF) | French Immersion Glossary |
| 3 | Comprehensive French/English math glossary (Grade 9) | French Immersion Glossary Grade 9 |
| 4 | Visual representation of mathematical reasoning progression | Math Reasoning Twist Model |
| 5 | Math vocabulary words for classroom use (Grade 4+) | Printable Word Wall |
| 6 | Custom Bingo cards with 2-D and 3-D shapes (25 unique cards, Grade 3,4) | Shapes 2D and 3D Bingo |
| 7 | French Bingo cards with 2-D and 3-D shapes (25 unique cards, Grade 3,4) | Bingo Forms 2D and 3D Vocab French |
| 8 | Tarsia printable puzzle (math vocabulary, Grade 6+) | Tarsia Math Vocabulary Dominoes |
| 9a | Note-making template for thinking tasks or consolidation of thin-sliced lessons (Grade 4+) | Big Four Template |
| 9b | Problem solving template for Rich Tasks, Problems of the Week (POTW), Grade 6+ | Numeracy Thinking Paper for POTW |
| 9c | One-column rubric for authentic problem-solving experiences that are connected to place, story, cultural practices, and perspectives relevant to local First Peoples communities, the local community, and other cultures (Grade 5+) | Math Lab Criteria Standards, w/ FPPL |
| 9d | One-page thinking paper for 3-Act Tasks (Grade 3+) | Three Act Recording Sheet |
| 9e | Instructions and examples of "Number Talks" instructional routine (Elementary) | Math Number Talks Provocations |
Authentic Tasks and Contextualized Learning Experiences
All activities that expand world knowledge (e.g. reading informational texts, learning new vocabulary, exploring new environments and places) are likely to be beneficial to the development of children's reasoning skills.
SD72 Teachers use a variety of critical thinking resources to teach reasoning and logical justification. Examples include Peter Liljedahl's Thinking Classroom approach, Carole Fullerton's "Good Questions", Number Talks, Esti-Mysteries, Open-Middle problems, University of Waterloo Problems of the Week, and Contextual Investigations (Math Labs).
 All four key curricular competencies can be assessed when students are engaged in rich thinking tasks.
All four key curricular competencies can be assessed when students are engaged in rich thinking tasks.
Many “Three-Act Tasks” combine both spatial and statistical reasoning
Understanding & Solving: Understand contextualized problems
Reasoning & Analyzing: Model mathematics in contextualized experiences
Communicating & Representing: Use mathematical vocabulary; explain and justify mathematical ideas and decisions
Connecting & Reflecting: Use mathematical arguments to support personal choices
Resources for Unpacking BCs Math Curricular Competencies:
| Understanding the BC Math Curriculum | Connecting BCs Curricular Competencies and Cognitive Rigor/Depth of Knowledge (DOK) |
| Big Ideas K-9 | Table: Depth of Knowledge and Math (11x17) |
| Foundational Numeracy Trajectories (multi-grade tables) | DOK questions article_w_matrix.docx |
| Mathematical Modelling Trajectory (All grades) | Robert Kaplinski’s DOK Matrix Exemplars |
| Measurement in Math Trajectory (All grades) | Article: Hess 7 Common Misconceptions About Rigor |
| Mathematics Learning Progressions K-4 (BCEd) | Mathematics Habits of Mind (Checklist & Reflection) |
| Classroom Assessment Resource Package - Math (BCEd) | |
| Grade Level Proficiency Descriptions (BCEd | |
| Numeracy Curricular Connections K-12 (BCEd) |
| Introducing the Notice & Wonder Protocol (from NCTM) | |
| |





 &
& 